Четири Боја Теорема

Source: http://people.math.gatech.edu/~thomas/FC/fourcolor.html

Ова страница даје кратак преглед новог доказа од четири Цолор теорема и алгоритам четири бојање пронашао Неил Робертсон , Даниел П. Сандерс , Паул Сеимоур и Робин Тхомас .

Преглед садржаја:

Историја.

Четири Боја проблем датира из 1852. када је Френсис Гатри, док је покушавао да обоји мапу округа Енглеске приметили да су четири боје довољан. Он је тражио од свог брата Фредерик да ли је истина да је било мапа може бити обојена коришћењем четири боје на такав начин да суседни региони (односно оне деле заједничку границу сегмент, а не само тачку) прима различите боје. Фредерик Гатри тада саопштио је претпоставку да онда је ДеМОрган. Прва штампана референца је због Цаилеиа 1878. године.

Годину дана касније први ‘доказ’ за Кемпе појавио; његова неисправност је истакао Хеавоод 11 година касније. Један пропали доказ је због Таит 1880; празнина у аргументу је истакао Петерсен у 1891. Оба се нису докази имали неку вредност, ипак. Кемпе открио оно што је постало познато као Кемпе ланаца и Таит наћи еквивалентан формулацију Фоур Цолор Тхеорем у смислу 3-ЕДГЕ-бојење.

Следећи велики допринос је дошао из Биркхофф чији је рад дозвољен Франклин 1922. да докаже да је четири боје претпоставка важи и за мапе са највише 25 региона. Такође је коришћен од стране других математичара да различите облике напретка о проблему са четири боје. Посебно смо треба поменути Хеесцх који је развио два главна састојке потребне за крајњи доказ – редуцибилити и пражњење. Иако је концепт редуцибилити је проучавана од стране других истраживача, као и, чини се да је идеја пражњења, од кључне важности за неминовност део доказа, је због Хеесцх, и да је он ко наслутио да је погодан развој ове методе би реши Фоур Цолор Проблем.

То је потврдио и Аппел и Хакен 1976, када је објавио свој доказ Фоур Цолор теорема [1,2] .

Зашто нови доказ?

Постоје два разлога зашто Апел-Хакен доказ није сасвим задовољавајући.

Део Апел-Хакен доказ користи рачунар, а не може да се утврди руком, и
чак и онај део који је наводно ручно може да се потврди је изузетно компликован и напоран, а колико знамо, нико га је проверио у целини.

Ми смо у ствари покушао да провери Апел-Хакен доказ, али је убрзо одустао. Провера део рачунара не би само потребно доста програма, али и инпутинг описе 1476 графиконима, а то није ни најконтроверзнији део доказа.

Одлучили смо да би било исплативије да раде наш сопствени доказ. То смо и урадили и дошли до доказа и алгоритам који су описани у даљем тексту.

Кратак опис доказа.

Основна идеја доказа је исти као Апел и Хакен је. Ми показују сет 633 “конфигурација”, и доказати сваки од њих је “свести”. То је технички концепт који подразумева да нема конфигурација са овом имовином може да се појави у минималној цоунтерекампле на четири Цолор теорема. Такође се може користити у алгоритму, јер ако редуцибле конфигурације појави у планарни графови Г, онда се може изградити у сталном времену мању планарни графови Г ‘тако да свака четири колорит Г “може бити конвертована у четворо- бојење Г у линеарном времену.

Познато је од 1913. да свака минимална цоунтерекампле на Фоур Цолор теорема интерно 6-повезан триангулацију. У другом делу доказа да докаже да је најмање један од наших 633 конфигурација се појављује у сваком интерно 6-повезан раванској троуглова (не мора да буде минимално цоунтерекампле на 4ЦТ). Ово се зове доказивање неминовност, и користи “метод пражњење”, први је предложио Хеесцх. Овде наш метод разликује од Аппел и Хакен.

Главне карактеристике нашег доказа.

Ми потврђују претпоставку о Хеесцх да у доказивању неминовност, А свести конфигурација се може наћи у другом насељу на “више оптерећени” темена; ово је како бисмо избегли “Иммерсион” проблеме који су били главни извор компликација за Аппел и Хакен. Наша неизбежна скуп има величину 633 у односу на скупу 1476 чланица Аппел и Хакен, а наш метод пражњење користи само 32 пражњења правила, уместо 300+ за Аппел и Хакен. Коначно, добијамо квадратну алгоритам за четири боје планарних графикона (описано касније), побољшање у односу на квартицним алгоритму Аппел и Хакен.

Конфигурације.

Скоро триангулатион је не-нула спојена лооплесс авион графикон таква да сваки ограничени регион троугао. Конфигурација К састоји од скоро триангулације Г и мапе г из В (г) у целих бројева са следећим особинама:

за сваки темена в, Г \ в има највише две компоненте, а ако постоје два, онда је степен в је г (в) -2,
за сваки темена в, ако в није инцидент са бесконачном региону, онда г (в) једнак степен в, и иначе г (в) већа од степен в; иу оба случаја г (в)> 4,
К има прстена величине најмање 2, где је прстен величине је дефинисана косовских да збир г (в) -дег (в) -1, сажета над свим вертицес в инцидент са бесконачном региону тако да Г \ в је повезан.

Приликом цртања слике конфигурације користимо конвенцију увео Хеесцх. Облици темена указују на вредност г (у) на следећи начин: Чврста црни круг значи г (В) = 5, тачка (или оно што се појављује на слици, као ни симбол уопште) означава г (у) = 6, шупаљ круг означава г (в) = 7, шупљи квадрат означава г (в) = 8, троугао означава г (в) = 9, а петоугао средства г (в) = 10. (Не треба темена в с г (у)> 11, и само један чвор са г (у) = 11, за које се не користи никакав посебан симбол.) На слици испод 17 наших 633 редуковати, конфигурација се приказују користећи назначену конвенцију. Цео скуп може погледати кликом овде . (Ми се односе на (3.2) нашег рада [7] за смислом “дебелих ивица” и “Халф-ивица” у овим сликама.)

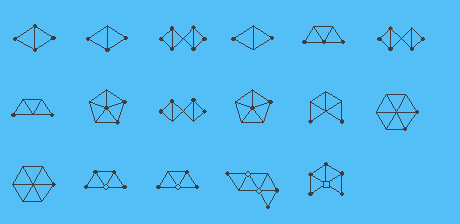
Свака конфигурација изоморфна једну од 633 конфигурација изложених на [7] се зове добра конфигурација. Нека је Т бити триангулација. Конфигурација К = (Г, г) се појављује у Т уколико Г је индукована подграф Т, сваки коначна регион Г је регион Т, и г (в) једнак степен В ин Т за сваки вертек В Г . Ми смо доказали следеће две изјаве.

Теорема 1. Ако Т је минимална цоунтерекампле на четири Цолор теорема, онда није добро конфигурација појављује у Т.

Теорема 2. За сваку интерно 6-повезан триангулације Т, добре конфигурације појављује у Т.

Из наведених две теореме следи да не постоји минимална цоунтерекампле, тако да је 4ЦТ је истина. Први доказ потребан компјутер. Други се може проверити руком у неколико месеци, или, помоћу рачунара, то се може проверити за око 20 минута.

Пражњење правила.

Нека је Т интерно 6 повезан триангулација. У почетку, сваки вертек в је додељен набој 10 (6-° (в)). Следи из ојлерова формула да је збир оптужби свих темена је 120; посебно, да је позитиван. Ми сада прерасподели оптужбе према следећим правилима, као што следи. Кад год Т има подграф изоморфна један од графикона у слици задовољавања спецификације степен (за темена В правилу са знаком минус поред против ово значи да је степен одговарајућег темена Т је највише вредности одређено обликом против, и аналогно за темена са знаком плус поред њих, једнакост је потребан за вертицес без знака поред њих) оптужби једне (два у случају првог правило) је за слање Рута ивица означен стрелицом.

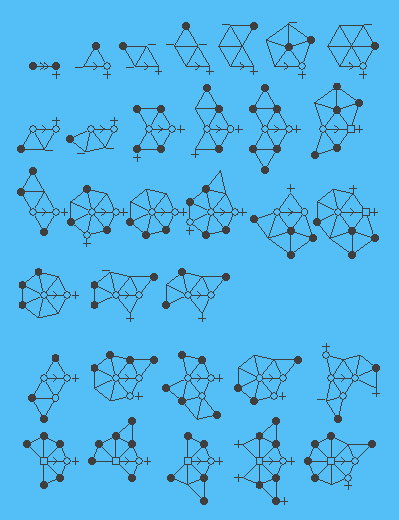
Ова процедура дефинише нови сет оптужби са истим укупне суме. Пошто је укупан збир позитиван, постоји чвор у у Т чија је нова оптужба је позитиван. Ми смо показали да је добра конфигурација се појављује у другом насељу против.

Ако је степен в је највише 6 или барем 12, онда се може видети прилично лако директним аргумент. За преосталих случајева, међутим, докази су много компликованије. Због тога, ми смо написали доказе у формалном језику, тако да се може проверити уз помоћ рачунара. Сваки појединачни корак од ових доказа је људски провјерити, али сами докази нису баш може да се потврди руком, због дужине.

Показивачи.

Теоријски део наше доказивања описана у [7] . 10-страница истраживање је доступан он-лине. Подаци рачунара и програми који се користе да се налази на анонимоус фтп сервер, али тај сервер је укинут. Исте датотеке су сада доступни од хттп://ввв.матх.гатецх.еду/~тхомас/ОЛДФТП/фоур/ и може се једноставно посматрати . Независно скуп програма је написао Гаспер Фијавз под вођством Бојан Мохар .

Квадратни алгоритам.

Улаз у алгоритам ће бити авион триангулација Г са н темена. (Ово је без губитка општости, као и сваки планарни графови може троугласти у линеарном времену.) Излаз ће бити бојење теменима Г са четири боје.

Ако Г има највише четири темена боја сваког врха другачије боје. У супротном уколико Г има вертек к степени К <5, а затим склоп Ц је окружују је `к-ринг”. Идите на к-прстена анализом испод. У супротном Г има минимални степен пет. За сваку темену налазимо своје наелектрисање као што је горе објашњено, и наћи вертекса В позитивно наелектрисање. Следи из нашег доказа о теореми 2. да било добро конфигурација појављује у другој околини в (што том случају се може наћи у линеарном времену) или к-прстена нарушавање дефиницију интерне 6 конекције може се наћи у линеарног времена. У овом другом случају идемо на анализи К-прстена испод, у првом случају примењујемо рекурзију до одређеног мањег графикона. Четворо-колорит Г се онда може конструисати из четири-бојење овом мањем графикона у линеарном времену.

Дат к-прстена Р крши дефиницију интерне 6 повезивања поступак развила Биркхофф могу користити. Примењујемо рецурсион до два пажљиво одабраних субграпхс од Г. четворочлану бојење Г онда могу бити конструисана од четири-бојила на два мања графикона у линеарном времену.

Дискусија.

Треба напоменути да су оба наша програми користе само цео број аритметика, па не морамо да се бави округли-офф грешака и сличних опасности са покретним зарезом аритметике. Међутим, аргумент може бити да је наш ‘доказ’ није доказ у традиционалном смислу, јер садржи кораке који никада не може бити верификована од стране људи. Посебно, нисмо доказали исправност преводилац смо саставили своје програме на, нити смо доказали непогрешивост хардвера смо водио своје програме на. Они се морају узети у вери, и да су разумљиво извор грешке. Међутим, са практичне тачке гледишта, шанса за грешке у компјутерским који се појављује стално на исти начин на све трчања наших програма на свим прикупљачи под свим оперативним системима да наши програми раде на је бесконачно мали у односу на шансе за људске грешке у истом износу slučaj провере. Поред овог хипотетичког могућности рачунар доследно даје погрешан одговор, остатак нашег доказа може да се утврди на исти начин као и традиционалне математички доказ. Ми признају, међутим, да провере компјутерски програм је много теже него проверу математички доказ исте дужине.

Захвалност.

Ми се задужио Тхомас Фовлер, Цхристопхер Царл Хецкман и Барретт Валлс за њихову помоћ у припреми ову страницу. Наш рад је делимично финансиран од стране Натионал Сциенце Фоундатион.

Референце.

K. Appel and W. Haken, Every planar map is four colorable. Part I. Discharging, Illinois J. Math. 21 (1977), 429-490.
K. Appel, W. Haken and J. Koch, Every planar map is four colorable. Part II. Reducibility, Illinois J. Math. 21 (1977), 491–567.
K. Appel and W. Haken, Every planar map is four colorable, Contemporary Math. 98 (1989).
G. D. Birkhoff, The reducibility of maps, Amer. J. Math. 35 (1913), 114-128.
H. Heesch, Untersuchungen zum Vierfarbenproblem, Hochschulskriptum 810/a/b, Bibliographisches Institut, Mannheim 1969.
A. B. Kempe, On the geographical problem of the four colors, Amer. J. Math., 2 (1879), 193-200.
N. Robertson, D. P. Sanders, P. D. Seymour and R. Thomas, The four colour theorem, J. Combin. Theory Ser. B. 70 (1997), 2-44.
N. Robertson, D. P. Sanders, P. D. Seymour and R. Thomas, A new proof of the four colour theorem, Electron. Res. Announc. Amer. Math. Soc. 2 (1996), 17-25 (electronic).
T.L. Saaty, Thirteen colorful variations on Guthrie’s four-color conjecture, Amer. Math. Monthly 79 (1972), 2-43.
T.L. Saaty and P. C. Kainen, The four-color problem. Assaults and conquest, Dover Publications, New York 1986.
P. G. Tait, Note on a theorem in geometry of position, Trans. Roy. Soc. Edinburgh 29 (1880), 657-660.
H. Whitney and W. T. Tutte, Kempe chains and the four colour problem”, in Studies in Graph Theory, Part II (ed. D. R. Fulkerson), Math. Assoc. of America, 1975, 378-413.